FIRST Tech Challenge Field Coordinate System Definition

Summary: The FIRST Tech Challenge Field Coordinate System is a Cartesian Coordinate System of three dimensions. The X and Y axes will refer to a position on the field and the Z axis a height above the field.

Scope

This document defines the Field Coordinate System for a FIRST Tech Challenge playing field. This definition can be used for consistent field-centric navigation, target localization and path planning.

Reference Frame

The reference frame for this definition is the field perimeter wall, adjacent to the red Alliance Area, known here after as the Red Wall. The definition is from the perspective of a person, standing outside the field, in the center of Red Wall, looking towards the center of the field.

Note

If the red Alliance Area is ever adjacent to two perimeter walls, the Red Wall will be the one with most contact with the Alliance Area. If the red Alliance Area is ever adjacent to two perimeter walls equally, then the most clockwise of the two walls will be considered to be the Red Wall.

Coordinate System

The Field Coordinate System is a Cartesian Coordinate System of three dimensions. X and Y will refer to a position on the field. Z will refer to a height above the field. You may use any length measure as long as the same measure is used for all three axes. The coordinates are ordered (X, Y, Z). Example: coordinate position (10, -10, 0) has X = 10, Y = -10 and Z = 0.

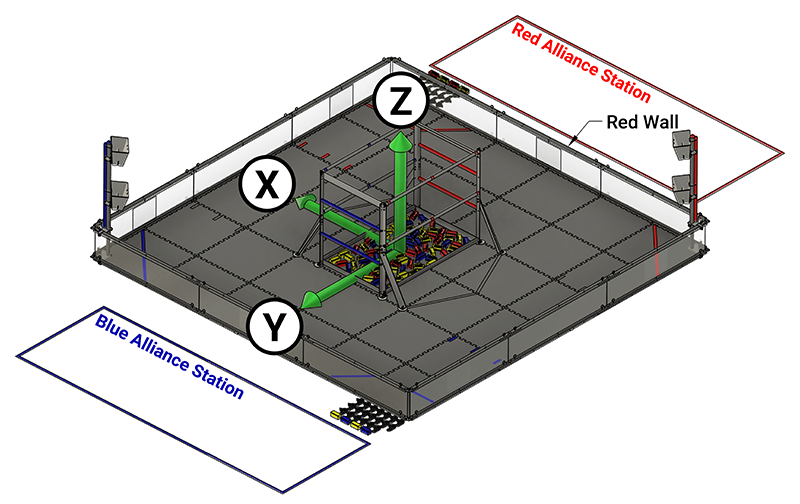
Origin

The 0,0,0 origin of the FIRST Tech Challenge coordinate system is the point in the center of the field, equidistant from all 4 perimeter walls (where the four center tiles meet). The origin point rests on the top surface of the floor mat.

X Axis

Looking at the origin from the Red Wall, the X axis extends through the origin point and runs to the right and left, parallel with the Red Wall. The X axis values increase to the right.

Y Axis

Looking at the origin from the Red Wall, the Y axis extends through the origin point and runs out and in, perpendicular to the Red Wall. Increasing Y values run out (away) from the Red Wall.

Z Axis

Looking at the origin from the Red Wall, the Z axis extends through the origin point and runs up and down in a vertical line. Increasing Z values extend upwards.

Rotation About Axes

When considering rotations about an axis, consider yourself looking down the axis from the positive end towards the origin. Positive rotations are then counterclockwise and negative rotations clockwise.

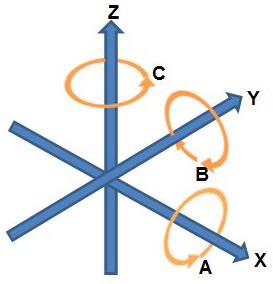
X, Y and Z coordinate axes.

Counterclockwise rotations about each axis

Imagine looking down the positive Z axis towards the origin. This would be like standing in the middle of the field looking down. A positive rotation about the Z axis would be counterclockwise.

Example: a robot spinning clockwise on the Field is making a negative rotation about the Z axis.

Field Configuration Examples

Below are two examples illustrating the Field Coordinate System for different FIRST Tech Challenge field configurations.

Note

In both field configurations the red Alliance is facing out along the positive Y axis, and the Z axis points up from the center of the field.

Diamond Field

A diamond field with X, Y and Z axes shown.

The FIRST RES-Q game field

In a diamond field configuration the two Alliance walls are adjacent. The field is rotated 45 degrees such that both Alliances face the audience. From the audience perspective the field forms a diamond shape. The Red Wall will be on the right as seen from the audience. The Y axis points across the field as seen from the Red Wall. The X axis points to the Blue Alliance.

Square Field

A square field with X, Y and Z axes shown.

The Into The Deep game field

In a square field configuration the two Alliances face each other across the field. The field is oriented such that the Red Wall is on the right as seen from the audience. The Y axis points across the field from the Red Wall towards the Blue Alliance. The X axis points away from the audience to the rear of the field.

Coordinate Position Example

Let’s consider the coordinates (0, -24, 26) in inches on the Into The Deep field, which is a square field. Given the order of coordinates then X = 0, Y = -24, and Z = 26.

The X axis value of 0 is located at the origin in the center of the field. The Y axis value of negative 24 would be located closer to the Red Wall, away from the origin by the width of one tile. This the center of the wall of the submersible structure on the red side of the field.

The Z axis value of 26 indicates the coordinates refer to the center and top of the Red Alliance “high chamber” (which is the higher of the two red crossbars).

Measured Values

The following metric values have been measured from a 2016 competition field. They are representative only, and should not be assumed to be exact, or guaranteed.

  • Distance between opposite inside faces of panels: 3580 mm, (if the field is assembled well: the straps give some adjustment tolerance)

  • Polycarbonate transparencies have a visible opening height of 255 mm

  • The top edge of transparencies is 30 mm from the top of the perimeter

  • Total perimeter height is 313 mm

  • Tiles are 13 mm thick

So, for a diamond field configuration, the corner of the field closest to the audience, at a height equal to the top of the perimeter wall, would have a coordinate position of: (-1790, 1790, 300) in millimeters.

Additional Information

See this Wikipedia article on Cartesian coordinate system in three dimensions. The Field Coordinate System rotation convention comes from the right hand rule of classic geometry.

Robots with a webcam can use AprilTags to determine where an AprilTag is located with respect to the robot. Since AprilTags are in known locations on the field, you can also determine the location of the robot on the field.

Robots can use an inertial measurement unit (IMU) to measure rotations about axes with respect to the robot. See IMU axes definition. The yaw value from the IMU, also known the heading, measures rotation about the Z axis which points up from the robot. You can use the IMU to determine which direction a robot is facing.